Linear algebra (unfinished)

IN MY OWN STYLE

Let’s go straight forward to the point.

Gauss-Jordan elimination

Gaussian elimination – to row echelon form

Gauss-Jordan elimination – to reduced row echelon form

1. linear system of equations
2. finding inverse matrix

Operations:

• rR
• R1 + R2
• R1 -> R2

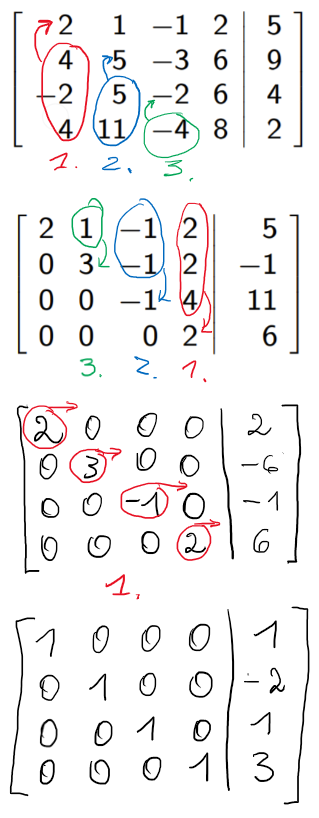
Gaussian elimination – tik pirmas etapas. Antras ir trečias etapas padaromi kartu, perkonvertavus į lygčių sistemą ir įsistatinėjant iš apačios į viršų

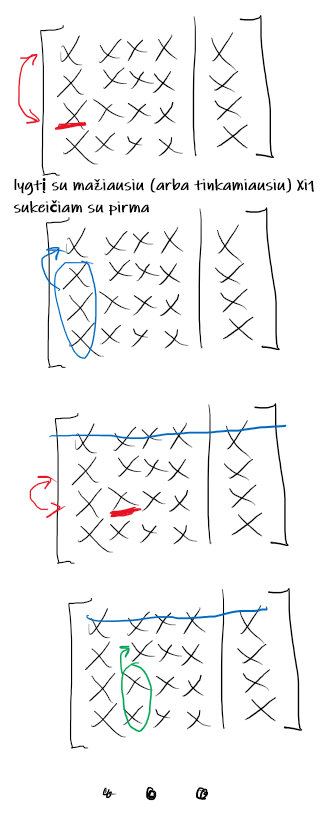
Pimojo etapo galimi tarpiniai veiksmai.

SOME DEFINITIONS:

Linear equation: $a_1x_1 + a_2x_2 + … + a_nx_n = b; (l_1, l_2, …, l_n)$

Types of equations:

No solution/there’s solution – inconsistent/consistent (neuderinta/suderinta) 1 solution/more than 1 solution – apibrėžta/neapibrėžta (ANGL?)

Matrices:

Triangular Trapezoidal – in gaussian elimination t substitution for laisvieji kintamieji in the last row (ANGL?) Row echelon form, Reduced row echelon form

Transpose

matrix of minors

matrix of coprimes

Inverse, Identity

invertible/singular matrix – has (/not) inverse (square; det(A) != 0)

Finding inverse

1. Gauss-Jordan

2. Adjancency matrix, matrix of coprimes, determinant

youtube link

Determinant

1. Rule of Sarrus

2. Laplace expansion

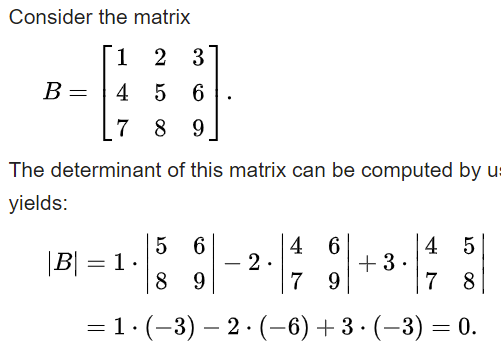
3. Unidentified

Let’s talk about matrices…

Matrix addition/subtraction

Matrix multiplication

Finding inverse matrix

Identity matrix Adjancency matrix Matrix of coprimes Determinant Gauss-Jordan elimination Vectors…

Cross product

Dot product

.

.

.

List:

Rank-nullity theorem

kernel, dimension, linear map, rank, null, nullspace, projection

matrix of minors, matrix of cofactors

Transpose

linear transformation

Links

Gauss-Jordan elimination youtube gaussian elimination youtube row echelon form, reduced echelon form gauss-jordan finding inverse